В языке ассемблера имеются средства записи
целых и вещественных чисел, а также
символьных строк и отдельных символов.
Целые числа могут быть со знаком и без знака,
а также записанными в двоично-десятичном
формате. Для целых чисел и символов в
составе команд микропроцессора и,
соответственно, в языке ассемблера, есть
средства обработки - анализа, сравнения,
поиска и проч. Для вещественных чисел таких
средств в самом микропроцессоре нет, они
содержатся в арифметическом сопроцессоре.
Поскольку программирование сопроцессора в
настоящей книге не рассматривается, то и
вещественными числами мы заниматься не
будем.
Рассмотрим сначала целые числа без знака и
со знаком. Числа без знака получили свое
название потому, что среди этих чисел нет
отрицательных. Это самый простой вид чисел:
они представляют собой весь диапазон
двоичных чисел, которые можно записать в
байте, слове или двойном слове. Для байта
числа без знака могут принимать значения от
00h (0) до FFh (255); для слова - от 0000h (0) до FFFFh (65535);
для двойного слова - от 00000000h (0) до FFFFFFFFh
(4294967295).
В огромном количестве приложений
вычислительной техники для чисел нет
понятия знака. Это справедливо, например,
для адресов ячеек памяти, кодов ASCII символов,
результатов измерений многих физических
величин, кодов управления устройствами,
подключаемыми к компьютеру. Для таких чисел
естественно использовать весь диапазон
чисел, записываемых в ячейку того или иного
размера. Если, однако, мы хотим работать как
с положительными, так и с отрицательными
числами, нам придется половину чисел из их
полного диапазона считать положительными,
а другую половину - отрицательными. В
результате диапазон изменения числа
уменьшается в два раза. Кроме того,
необходимо предусмотреть систему
кодирования, чтобы положительные и
отрицательные числа не перекрывались.
В вычислительной технике принято
записывать отрицательные числа в так
называемом дополнительном коде, который
образуется из прямого путем замены всех
двоичных нулей единицами и наоборот (обратный
код) и прибавления к полученному числу
единицы. Это справедливо как для байтовых (8-битовых)
чисел, так и для чисел размером в слово или в
двойное слово (рис. 2.8)

Рис. 2.8. Образование отрицательных чисел
различного размера.
Такой способ образования отрицательных
чисел удобен тем, что позволяет выполнять
над ними арифметические операции по общим
правилам с получением правильного
результата. Так, сложение чисел +5 и -5 дает 0;
в результате вычитания 3 из 5 получается 2;
вычитание -3 из -5 дает -2 и т.д.
Анализируя алгоритм образования
отрицательного числа, можно заметить, что
для всех отрицательных чисел характерно
наличие двоичной единицы в старшем бите.
Положительные числа, наоборот, имеют в
старшем бите 0. Это справедливо для чисел
любого размера. Кроме того, из рис. 2.8 видно,
что для преобразования отрицательного 8-битового
числа в слово достаточно дополнить его
слева восемью двоичными единицами. Легко
сообразить, что для преобразования
положительного 8-битового числа в слово его
надо дополнить восемью двоичными нулями. То
же справедливо и для преобразования слова
со знаком в двойное слово со знаком, только
добавить придется уже не 8, а 16 единиц или
нулей. В системе команд МП 86 и,
соответственно, в языке ассемблера, для
этих операций предусмотрены специальные
команды cbw и cwd.
Следует подчеркнуть, что знак числа условен.
Одно и то же число, например, изображенное
на рис. 2.8 8-битовое число FBh можно в одном
контексте рассматривать, как отрицательное
(-5), а в другом - как положительное, или,
правильнее, число без знака (FBh=251). Знак
числа является характеристикой не самого
числа, а нашего представления о его смысле.
На рис. 2.9 представлена выборочная таблица
16-битовых чисел с указанием их машинного
представления, а также значений без знака и
со знаком. Из таблицы видно, что для чисел со
знаком размером в слово диапазон
положительных значений простирается от 0 до
32767, а диапазон отрицательных значений - от -1
до -32768.
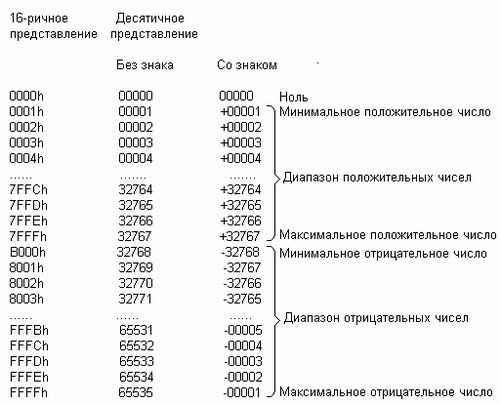
Рис. 2.9. Представление 16-битовых чисел
без знака и со знаком.
На рис. 2.10 представлена аналогичная
таблица для 8-битовых чисел. Из таблицы
видно, что для чисел со знаком размером в
байт диапазон положительных значений
простирается от 0 до 127, а диапазон
отрицательных значений - от -1 до -128.

Рис. 2.10. Представление 8-битовых чисел
без знака и со знаком.
Среди команд процессора, выполняющих ту
или иную обработку чисел, можно выделить
команды, безразличные к знаку числа (например,
inc, add, test), команды, предназначенные для
обработки чисел без знака (mul, div, ja, jb и др.), а
также команды, специально рассчитанные на
обработку чисел со знаком (imul, idiv, jg, jl и т.д.).
Особенности использования этих команд
будут описаны в следующей главе.
Рассмотрим теперь другой вид представления
чисел - двоично-десятичный формат (binary-coded
decimal , BCD), используемый в ряде прикладных
областей. В таком формате выдают данные
некоторые измерительные приборы; он же
используется КМОП-часами реального времени
компьютеров IBM PC для хранения информации о
текущем времени. В МП 86 предусмотрен ряд
команд для обработки таких чисел.
Двоично-десятичный формат существует в
двух разновидностях: упакованный и
распакованный. В первом случае в байте
записывается двухразрядное десятичное
число от 00 до 99. Каждая цифра числа занимает
половину байта и хранится в двоичной форме.
Из рис. 2.11 можно заметить, что для записи в
байт десятичного числа в двоично-десятичном
формате достаточно сопроводить
записываемое десятичное число символом h.

Рис. 2.11. Упакованный двоично-десятичный
формат.
В машинном слове или в 16-разрядном
регистре можно хранить в двоично-десятичном
формате четырехразрядные десятичные числа
от 0000 до 9999 (рис.2.12).
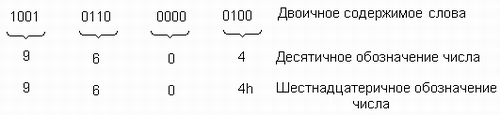
Рис. 2.12. Запись десятичного числа 9604 в
слове.
Распакованный формат отличается от
упакованного тем, что в каждом байте
записывается лишь одна десятичная цифра (по-прежнему
в двоичной форме). В этом случае в слове
можно записать десятичные числа от 00 до 99 (см.
рис. 2.13)

Рис. 2.13. Запись десятичного числа 98 в
распакованном виде.
При хранении десятичных чисел в
аппаратуре обычно используется более
экономный упакованный формат; умножение и
деление выполняются только с
распакованными числами, операции же
сложения и вычитания применимы и к тем, и к
другим. Примеры операций с двоично-десятичными
числами будут рассмотрены в следующей
главе.














