Программирование ХММ-расширения
Новые сапоги всегда жмут.
Козьма Прутков
Необходимо отметить тот факт, что фирма Intel — не единственная из фирм, разрабатывающих микропроцессоры, активно работает над проблемой обработки больших массивов однородной информации. Не секрет, что постоянным соперником фирмы Intel по вопросам архитектуры микропроцессора является фирма AMD. Между ними по различным направлениям идет постоянная борьба за рынок компьютеров архитектуры х86. Мы не будем рассматривать ее хронологию, уделим внимание лишь тому, для чего и в какой форме в архитектуре микропроцессоров этих фирм появились средства для потоковой обработки данных с плавающей точкой или SSE (Streaming SIMD Extensions). Толчком к развитию SIMD-технологий (в том числе и целочисленных) стали задачи с большими объемами однородных исходных данных простой структуры. Основные области, где встречается такая информация, — Интернет и компьютерные игры. Именно здесь возникает множество задач по обработке звука, видео, графики. Если рассматривать современные компьютерные игры, то в них активно используются мощности со-
процессора для производства расчетов ЗО-объектов в трехмерном пространстве (отсюда, кстати, и название — 3DNow!). Архитектура и производительность стандартного сопроцессора не обеспечивают с нужной эффективностью эти расчеты. Фирмы — производители микропроцессоров активно начали поиск технологий, которые позволили бы увеличить производительность подсистемы для расчетов с плавающей точкой. Известно несколько путей повышения эффективности расчетов подобного рода: увеличение тактовой частоты, уменьшение задержек выполнения команд в сопроцессоре, конвейеризация вычислений с плавающей точкой, реализация SIMD-технологии, использование параллельных конвейерных устройств для расчетов с плавающей точкой. Среди этих путей фирмы Intel и AMD выбрали свои. Тактовую частоту работы микропроцессора постоянно повышают обе фирмы, чему мы являемся заинтересованными свидетелями. Что же касается подсистемы обработки данных с плавающей точкой, то архитектурно они реализованы по-разному. Так, фирма Intel пошла по пути конвейеризации вычислений с плавающей точкой и реализации SIMD-технологии вычислений с плавающей точкой. Фирма AMD работает над уменьшением задержек выполнения команд в сопроцессоре и над реализацией SIMD-технологии вычислений с плавающей точкой. Эти технологии реализованы в микропроцессорах Pentium III фирмы Intel и Atlon фирмы AMD, но они не совсем одинаковы. Архитектура целочисленного MMX-расширения у этих микропроцессоров совпадает (в семействе AMD целочисленное MMX-расширение появилось в микропроцессоре AMD Кб (ММХ)), что же касается архитектуры ХММ-расширения с плавающей точкой, то здесь различия более существенные начиная с их названий. Потоковое расширение с плавающей точкой микропроцессора Atlon называется 3DNo\v! и включает 21+5 команд. 21 команда расширения 3DNow! существовала в предыдущем микропроцессоре AMD K6-2-3DNow!, 5 команд этого расширения были введены дополнительно в расширение 3DNow! микропроцессора AMD Athlon. Потоковое расширение микропроцессора Pentium III фирмы Intel называется Streaming SIMD Extensions и включает 70 команд. Стоит отметить, что не все из этих 70 команд являются командами SSE-расширения: 50 команд относятся непосредственно к блоку SSE-расширения, то есть являются командами SIMD с плавающей точкой, 12 команд дополняют систему команд целочисленного MMX-расширения и 8 команд относятся к системе кэширования.
Велики различия в физической реализации расширений 3DNow! и Streaming SIMD Extensions. SSE-расширение фирмы Intel выполнено в виде отдельного блока, расширение 3DNow процессоров AMD реализовано на базе стандартного сопроцессора. Второе важное отличие — размерность регистров. Их количество совпадает для обоих расширений. Размерность регистров SSE-расширения — 128 бит, то есть 4x32 бита в формате короткого слова с плавающей точкой. Размерность регистров расширения 3DNow — 64 бита, то есть 2x32 бита в формате короткого слова с плавающей точкой. Таким образом, SSE-расширение процессоров Intel имеет вдвое больше регистров, чем 3DNow!-pacurapeHne процессоров AMD. Выводы из этого делайте сами. К примеру, задачи трехмерной графики активно работают с матрицами 4x4 (см. ниже). В процессе написания программы для 3DNow!-pacnrapeHra процессора AMD пропэаммист вынужден постоянно решать проблему нехватки регистров в 3DNow! со всеми вытекающими последствиями, в том числе и для красоты алгоритма. Реализация SSE-расширения
в виде отдельного блока увеличивает параллельность вычислений в процессоре, так как одновременно могут выполняться команды целочисленного устройства, сопроцессора и SSE-расширения. Читатель может возразить, что, несмотря на все эти недостатки, результаты тестов в различных изданиях говорят о том, что зачастую не наблюдается существенного различия в производительности микропроцессоров фирм Intel и AMD одного класса. На взгляд автора, это следствие I того, что фирме AMD удается компенсировать существующие архитектурные различия хорошей проработкой схемотехнических проблем микроархитектурного уровня. Дальнейшее изложение будет основано на базе ХММ-расширения Pentium III — то есть SSE-расширения.
Наибольшую выгоду от использования SSE-расширения Pentium получают задачи трехмерной графики, а также приложения 2D- и 2.50-графики, использующие векторную графику в фоновой части изображения. При желании программист может найти полезные особенности команд ХММ-расширения для использования их при разработке приложений из других предметных областей. Один из основных признаков, на которые стоит обратить внимание при выборе средств реализации, — наличие матричных преобразований, таких как умножение, транспонирование, сложение, вычитание матриц, умножение матрицы на вектор, световые преобразования, подобные преобразованиям между цветовыми моделями RGB и CMYK, и т. п.
В заключение этой части обсуждения отметим, что набор SIMD-инструкций ХММ-расширениия микропроцессора Intel (и AMD тоже) бесполезен без соответствующей программной поддержки. Далее рассмотрим, каким образом использовать ХММ-команды в программах на языке ассемблера. Следует отметить, что данный материал может быть полезен не только для программистов на языке ассемблера, но и для тех, кто пишет программу на языке высокого уровня. Благодаря ассемблерным вставкам или внешним ассемблерным процедурам программист может использовать возможности новых процессоров, не дожидаясь появления новой версии компилятора, поддерживающего эти возможности. Это также имеет место с Pentium III. Оперативно отслеживать процессорные новшества удается только компилятору С/С ++ фирмы Intel и макроассемблеру фирмы Microsoft, который поддерживает новые команды SSE начиная с версии 6.1 Id и выше. Но известно, что далеко не все программисты на С и ассемблере предпочитают эти компиляторы другим аналогичным средствам разработки. Что же делать таким программистам, в частности программирующим на ассемблере с использованием пакета TASM? Ответ один — выкручиваться. Как? Этому и будет посвя-гцено обсуждение ниже. Оно будет логически состоять из двух частей. В первой части мы сделаем вид, что ничего не происходит и транслятор TASM поддерживает любые команды процессора Pentium III. Во второй части мы действительно поможем TASM это сделать.
Вначале разберем порядок описания данных, которыми манипулируют ХММ-команды Pentium III, а затем рассмотрим несколько примеров их использования.
Описание упакованных и скалярных данных
Описание ХММ-данных в приложении обычно производится в одном из двух форматов:
- в массиве структур;
- в структуре, элементами которой являются массивы.
Описание точек изображения в трехмерном пространстве принято задавать в виде четырехмерного вектора (x.y.z.w). Это связано с тем, что проективные преобразования, необходимые для показа изображения с различных точек зрения, наиболее просто описываются матрицами 4x4. Используя перечисленные выше форматы задания ХММ-данных, совокупность точек в трехмерном пространстве можно описать двумя способами:
- первый способ — для каждой точки определить свой экземпляр структуры:
point 3D struc х del 0.0 у dd 0.0 z dd 0.0 w dd 0.0
ends .data pi point_3D 4 dup (<>) ;описание пирамиды массивом структур.
;каждая из которых описывает одну из 4 вершин
- В второй способ — все точки описать одной структурой, элементами которой являются массивы координат x,y,z,w:
pri sm_point_3Dstruc x dd 4 dup (0.0) у dd 4 dup (0.0) z dd 4 dup (0.0) w dd 4 dup (0.0)
ends .data prism prism_point_3D<> структура, описывающая треугольную пирамиду (4 вершины)
Приведенные выше примеры описания пирамиды иллюстрирует рис. 10.1.
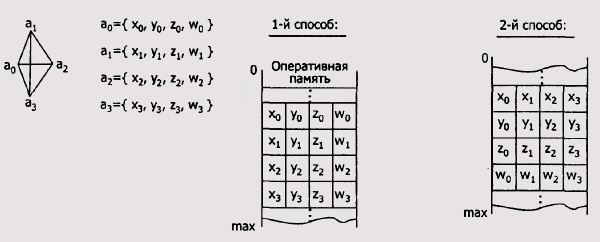
Рис. 10.1. Расположение в памяти описания вершин пирамиды
В большинстве приложений используется первый способ представления ХММ-данных, хотя он считается и менее эффективным. При необходимости можно произвести преобразование представления данных из одного способа в другой. Вариант такого преобразования показан в программе ниже. ;рrg10 01.asm - программа преобразования представления ХММ-данных :из одного способа представления в другой.
prizm struc
union
struc структура, описывающая треугольную пирамиду (1 способ)
xyzwl dd 0.0
xyzw2 dd 0.0
xyzw3 dd 0.0
xyzw4 dd 0.0
ends
struc структура, описывающая треугольную пирамиду (2 способ) х dd 4 dup (0.0) у dd 4 dup (0.0) z dd 4 dup (0.0) w dd 4 dup (0.0)
ends
ends ;конец объединения
ends .data
prizm_l prizm <> :экземпляр объединения .code
преобразование представлений вершин пирамиды (на месте)
lea si.prizm_l
movlps rxmm0.[si] ;rxmm0=? ? уО xO
movhps rxmmO,[si+16] ;rxmm0= yl xl yO xO
movlps rxmm2.[si+32] ;rxmm2« ? ? y2 x2
movhps rxmm2.[si+48] ;rxmm2= уЗ хЗ у2 х2
movaps rxmml.rxmmO :rxmml= yl xl yO xO
shufps rxmmO.rxmm2.88h :rxmm0= x3 x2 xl xO
shufps rxmml.rxmm2.0ddh ;rxmml= уЗ у2 yl yO
movlps rxmm2.[si+8] ;rxmm2=? ? wO zO
movhps rxmm2.[si+24] :rxmm2= wl zl wO zO
movlps rxmm4.[si+40] ;rxmm4= ? ? w2 z2
movhps rxmm4,[si+56] ;rxmm4= w3 z3 w2 z2
movaps rxmm3.rxmm2 ;rxmm3= wl zl wO zO
shufps rxmm2.rxmm4.88h :rxmm2= = z3 z2 zl zO
shufps rxmm3.rxmm4.0ddh ;rxmm3= w3 w2 wl wO . -на выходе получим следующее состояние ХММ-регистров:
;RXMM0= хЗ х2 xl xO. RXMM1= уЗ у2 yl yO. RXMM2= ¦ z3 z2 zl zO. RXMM3= w3 w2 wl wO :теперь их необходимо сохранить в памяти:
movups [si].rxmm0
movups [si+16].rxmml
movups [si+32].rxmm2
movups [si+48].rxmm3
Описание скалярных данных намного проще - это обычные значения с плавающей точкой в коротком формате:
.data
seal real dd 1.0 :пример описания скалярного ХММ-значения;
Примеры использования команд ХММ-расширения
Ниже будут рассмотрены несколько типовых примеров использования команд ХММ-расширения. Основная цель — демонстрация методики работы с основными группами команд ХММ-расширения. Начнем с реализации простейших операций — сложения и умножения.
Сложение и умножение двух упакованных ХММ-значений
Задача — вычислить скалярное произведение двух векторов, каждый из которых состоит из 4 вещественных чисел в коротком формате. Если в качестве таких векторов взять два вектора А и В, то их произведение вычисляется по формуле: АхВ = aoxbo+aixbi+a2xb2+a3xb3- В программной реализации с использованием ХММ-команд это выглядит так, как показано ниже.
:prg10_02.asm - программа вычисления скалярного произведения двух векторов.
.data
xmm_pack_l dd 1.0. 2.0. 3.0. 4.0
xmm_pack_2 dd 5.0. 6.0. 7.0. 8.0
rez_sum dd 0.0 результат сложения .
.code
movaps rxmmO.xrom_pack_l ;RXMM0= 4.0. 3.0, 2.0, 1.0 mulps rxmm0.xinTi_pack_2 :RXMM0= 4.0x8.0. 3.0x7.0. 2.0x6.0, 1.0x5.0 movaps rxmml. rxmmO :RXMM1= 4.0x8.0, 3.0x7.0. 2.0x6.0. 1.0x5.0
shufps rxmml.rxmml.4eh ;RXMM1= 2.0x6.0, 1.0x5.0. 4.0x8.0. 3.0x7.0 addps rxmmO. rxmml :складываем:
;RXMM0= 4.0x8.0. 3.0x7.0. 2.0x6.0, 1.0x5.0
J +
:RXMM1= 2.0x6.0. 1.0x5.0. 4.0x8.0. 3.0x7.0
:RXMM0- 4.0x8.0+2.0x6.0. 3.0x7.0+1.0x5.0, 2.0x6.0+4.0x8.0. 1.0x5.0+3.0x7.0
:или
;RXMM0= 44.0. 26.0, 44.0. 26.0
movaps rxmml, rxmmO :RXMM1= 44.0, 26.0, 44.0, 26.0
shufps rxmml.rxmml.llh :RXMM1= 26,0. 44.0. 26.0. 44.0
addps rxmmO. rxmml :складываем: ;RXMM0= 44.0. 26.0. 44.0, 26.0
; +
;RXMM1= 26.0, 44.0, 26.0, 44.0
:RXMM0= 70.0. 70.0, 70.0, 70.0 сохраняем результат movss rez_sum.rxmm0
Умножение матрицы на вектор
Умножение матрицы на вектор — наиболее характерная операция для вычислений в области машинной графики. Существуют различные способы формирования трехмерного изображения. В наиболее простом случае изображение на экране задается в виде опорных точек. К примеру, рассмотрим случай, когда на экране дисплея находится трехмерное изображение, состоящее из отрезков прямых. Необходимая для его формирования информация хранится в памяти как список опорных точек — концов отрезков. Если изображение дается в трехмерном изображении, то описание каждой точки удобно задать в виде четырехмерного вектора (х, у, z, w). Включение в трехмерный вектор (х, у, z) дополнительной координаты w объясняется тем, что проективные преобразования, необходимые для показа изображения с различных точек зрения, описываются матрицами 4x4. Поэтому для удобства реализации проективных преобразований, зачастую сопровождаемых операциями умножения матриц и векторов, трехмерный вектор (х, у, z) представляют в виде четырехмерного вектора (х, у, г, w), где значение w обычно принимается равным 1. Для выполнения самого преобразования, подготовленная заранее матрица преобразования умножается на этот вектор, в результате чего получается четырехмерный вектор (х1, у', г , w'). Для обратного перехода к требуемому трехмерному вектору необходимо разделить координаты х', у', г на w', после чего удалить четвертую координату w'.
Матрица М преобразования и вектор V имеют следующий вид:
m00 m01 m02 m03 x
mio mu m12 m13 у
m20 m21 m22 m23 z
m30 m31 m32 m33 w=l
Преобразования координат выполняются по формулам:
х' ™ xxm0o+yxni01+zxm02+lxm03
у' » xxm+yxnid+zxm+lxm
г = xxm20+yxm21+zxm22+lxm23
w' = xxm30 +yxm31+zxm32+lxm33
Для получения преобразованных координат в виде трехмерного вектора (x,y,z) делим х', у', z' на w':
х = x'/w' = (ххт00+ухт01+гхт02+1хт0з)/(ххт30+ухт31+гхт32+1хт3з)
У = У'/w' = (xxmlo+yxm))+zxm,2+lxm13)/(xxm3O+yxm31+zxm32+lxm33)
z - z'/w' = (xxm20+yxm2i+zxm22+lxm23)/(xxm30+yxm31+zxm32+lxm33)
Элементы матрицы И векторов представлены числами с плавающей точкой в коротком вещественном формате (4 байта).
Ниже приведены два варианта программы умножения матрицы на вектор — один с использованием стандартного сопроцессора, другой с использованием команд ХММ-расширения (с помощью профайлера можно сравнить скорость преобразования). Результирующий трехмерный вектор замещает исходный.
Умножение матрицы 4x4 на четырехмерный вектор (стандартный сопроцессор)
Подпрограмма состоит из двух частей. В первой части вычисляется собственно произведение четырехмерной матрицы на четырехмерный вектор. Во второй части полученный четырехмерный вектор преобразуется влрехмерный путем деления его компонентов на его четвертую координату. :prgl0_05.asm - программа поворота изображения на месте :с использованием средств стандартного сопроцессора.
t :
:координаты квадрата (необходимо инициализировать) xO.yO.xl.yl.x2.y2.x3.y3 mas_xy dd 8 dup (0.0)
a dd 0.0 :угсл (необходимо инициализировать) .code
lea si.mas_xy
mov ex.4 :цикл 4 раза - по количеству вершин
firm ;вычисляем sin а и cos a;
fid a ;включаем а стек угол
fsin вычисляем sin a
fxch ;меняеи st(0)<->st(l)
fcos ;вычисляем cos a
fxch ;меняем st(0)<->st(l)
fstp a :выталкиваем а :поворот изображения cycl: fild word ptr [si] :включить в стек координату х элемента
fild word ptr [si+2] :включить в стек координату у элемента
fid St(l) ;дублируем их
fid st(l)
fmul st.st(5) вычислить y*sin
fxch :меняем st(0)<->st(l)
fmul St.st(4) вычислить x'cos
fadd :новая координата х
fistp word ptr[si] :передать новую координату х в память
fmul st.st(2) вычислить y*cos
fxch ' ;меняем st(0)<->st(l)
fmul St.StO) .-вычислить x*sin
fsubr .новая координата у
fistp word ptr[si*4] ;передать ее в память
add si.8 ;продвинуть указатель массива mas_xy
loop cycl повторить еще 3 раза :в mas_.ху преобразованные для поворота координаты квадрата
Поворот изображения (ХММ-расширение)
:prgl0_06.asm - программа поворота изображения на месте
:с использованием средств ХММ-расширения.
.data
:ALIGN 16
:координаты квадрата (необходимо инициализировать) хО,уО,х1.у1.х2.у2.х3.уЗ
mas_xy dd 8 dup (0.0)
a dd 0.0 :угол (необходимо инициализировать)
sin_a dd 0.0
cos_a dd 0.0
null dd 0.0
. code
:.........
lea esi.raas_xy
mov ecx.4 :цикл 4 раза - no количеству вершин
finit вычисляем sin а и cos a;
fid a :включаем в стек угол
fsin вычисляем sin a
fxch ;меияем st(Q)<->st(l)
fcos ;вычисляем cos a
fxch ;меняем st(0)<->st(l;
fstp a ;выталкиваем а
fstp cos_a ; выталкиваем cos__a
fstp sin_a ;выталкиваем sin_a
;поворот изображения
;готовим xmm-регистр RXMM2 со значениями углов movlps rxmm2.sin_a
movhps rxmm2,sin_a ;RXMM2= cos_a sin_a cos_a sin__a
movss rxmm2.nul1
siibss rxmm2.sin_a ;RXMM2= cos_a sin_a cos_a -sin_a
cycl: movlps rxmmO.Lesi] :RXMM0= ? ? yi xi movhps rxnwO.Cesi] ;RXMM0= yi xi yi xi
shufps rxmmO.rxmmO.ObOh :RXMM0= xi yi yi xi
mulps rxmmO.rxnm2 ;RXMM0-RXMM0*RXMM2= xi*cos_a yi*sin_a yi* cos_a xi*(-sin_a)
shufps rxmml.rxmmO.31h ;RXMM1=? xi*cos_a ? yi* cos_a
addps rxmmO.rxmml :RXMM0= ? (xi*cos_a+yi*sin_a) ? (yi* cos_a+xi*(-sin_a))
shufps rxmmO.rxmmO.2 ;RXMM0=- ? ? (yi* cos_a+xi*(-sin_a)) (xi*cos_a+yi*sin_a) сохраняем результат: movlps [esi].rxnim0 ;готовимся к вычислению нового положения для следующей координаты
add esi,8 1oop cycl
На этом мы закончим рассмотрение примеров программирования ХММ-расширения. При разработке приведенных выше программ мы считали, что используемый нами транслятор ассемблера поддерживает любые команды микропроцессора Intel, в том числе и ХММ-команды. Реально ситуация далека от этой идеальной картины. Мы уже упоминали, что если транслятор MASM (фирмы Microsoft) пытается поспевать за процессом развития системы команд, то для TASM дело обстоит несколько хуже. Другие фирмы-разработчики трансляторов ассемблера мы не рассматриваем (не потому, что они хуже — просто обсуждение достоинств и недостатков трансляторов ассемблера не является предметом данной книги). Настало время, не меняя любимого транслятора, помочь ему понять неизвестные команды микропроцессора. Для этого в следующей части данного раздела мы выработаем соответствующую методику.
|








