Поиск с предварительным анализом искомой подстроки
Против незнания есть только одно средство — знание.
Истинное же знание может быть достигнуто
только через личное совершенствование.
Л. Н. Толстой
Основу материала этого раздела составляет алгоритм КМП-поиска. Имя «КМП» является выборкой первых букв фамилий его создателей: Д. Кнута, Д. Мориса
и В. Пратта. В основе алгоритма КМП-поиска лежит идея о том, что в процессе просмотра строки S с целью поиска вхождения в нее образца Р становится известной информация о просмотренной части. Работа алгоритма производится в два этапа.
- 1. Анализируется строка-образец Р. По результатам анализа заполняется вспомогательный массив смещений D.
2. Производится поиск в строке S с использованием строки-образца Р и массива смещений D.
Ниже приведена программа, реализующая алгоритм КМП-поиска.
//рrg4_73_КМР - программа на псевдоязыке поиска строки Р в строке S
//по алгоритму КМП-поиска. Длина S фиксирована. ..<. ¦ ¦¦ ¦¦
// Вход: S и Р - массивы символов размером N и М байт (M=<N)
II Выход: сообщение о количестве вхождений строки Р в строку S.
ПЕРЕМЕННЫЕ .
INT_BYTE s[n]://0=<i<N-l
INT_BYTE p[m]://0-<j<M-l .
INT_BYTE d[ml://массив смещений
INT_BYTE k=-l: i=0: j-0 //индексы
НАЧ_ПРОГ .
//этап 1: формирование массива смещений d
' И j:-0; k:-l:'d[0]
ПОКА ДЕЛАТЬ
НАЧ_БЛОК 1 .
nOKA~"((k>=0)M(p[j]<>p[k])) k:-d[k]
j:=j+l: k:-k+l :
ЕСЛИ p[j]-p[k] TO d[j]:-d[k] .
ИНАЧЕ d[j]:-k .
кон_блок_1 .
//этап 2: поиск
i:-0: j:-0: k:=0
ПОКА ((j<M)M(i<N)) ДЕЛАТЬ
НАЧ_БЛОК_1 ' '" '"'
ПОКА ((j>=O)H(s[i]<>p[j])) j:-dtj]
j:-j+l: i:=i+l
КОН_БЛОК_1
ЕСЛИ j=M TO зывод сообщения об удаче поиска
ИНАЧЕ вывод сообщения о неудаче поиска КОН ПРОГ
jmpm3
ml: :ЕСЛИ j=M TO вывод сообщения об удаче поиска :вывод сообщения о результатах поиска
cmp si ,len_p
jneexit_f :ИНАЧЕ вывод сообщения о неудаче поиска
inc count
cmp di ,len_s
jgeexit_f
xor si ,si
jmp m34
exit_f:add count.30h :вывод сообщения mes на экран
Подробно, хотя и не очень удачно, алгоритм КМП-поиска описан у Вирта [4]. Этот алгоритм достаточно сложен для понимания, хотя в конечном итоге его идея проста. Центральное место в алгоритме КМП-поиска играет вспомогательный массив D. Поясним его назначение. Массив D содержит значения, которые нужно добавить к текущему значению j в позиции первого несовпадения символов в строке S и подстроке Р (рис. 4.1).

Рис 4.1. Пример КМП-поиска
Из обсуждения выше можно сделать два вывода — один приятный, другой не очень. Во-первых, явное достоинство этого метода в том, что исключены возвраты
:задаем массив S
s db "fgcabceabcaab"
Len_S=$-s :N=Len_S
db Count db 0 ;счетчик вхождений Р в S
Db " раз(а)$"
d db 255 dup (0) вспомогательный массив ¦' ¦ k db 0 .,.,.,'
.code
:этап 1 - заполнение массива D значением М - размером образца для поиска
mov ex.255 :размер кодовой таблицы ASCII
moval.lenjj :ДЛЯ j=0 ДО 255 ДЕЛАТЬ
lea di .d rep stosb :d[j]:=M
:цикл просмотра образца и замещение некоторых элементов d значениями смещений :(см. пояснение за текстом программы)
xor si .si ; j:=0 '
cycll: :ДЛЯ j>0 ДО М-2 ДЕЛАТЬ ..>;
empsi ,1еп_р-1
jgee_cycll
mov al ,p[si]
movdi.ax
movbl.len_p
decbl
subbx.si
movd[di],bl :d[p[j]]:-MrJ-l:!
inc si ¦, -.r
e_cycll: ://этап 2: поиск
movdi,len_p
cycl 2:,; ПОВТОРИТЬ - цикл пока (j>-0)WW(I<n) . movsi.len_p :j:=M . , ;¦
movbx.di :k:=I . '.
cycl3: :цикл пока (j>-O)MJlH(p[j]~p[k])
decbx :k:-k-l . ' '¦' '
dec si :j:-j-l cmp si.0 jl m2
mov al.p[si] cmps[bx].al jnem2 jmpcycl3 m2: ;i:-i+d[s[i-: push di dec di
mov al,s[di] mov di ,ax moval .dfdi] popdi
add di .ax cmp s i, 0 jl ml cmp di .len_s
jg exi t_f
jmp cycl2 ml: ;вывод сообщения о результатах поиска
inc count
jmpcycl2 exit_f:add count.30h
lea dx.mes
mov ah.09h
int 21h exit: Идея алгоритма БМ-поиска в том, что сравнению подвергаются не первые, а последние символы образца Р и очередного фрагмента строки S. Если они не равны, то сдвиг в строке S осуществляется сразу на всю длину образца. Если последние символы равны, то сравнению подвергаются предпоследние символы, и т. д. При несовпадении очередных символов величина сдвига извлекается из таблицы D, которая, таким образом, выполняет ключевую роль в этом алгоритме. Заполнение таблицы происходит на основе конкретной строки-образца Р следующим образом. Размер таблицы определяется размером алфавита, то есть количеством кодов символов, которые могут появляться в тексте. В нашем случае мы отвели под таблицу D память длиной, равной длине кодовой таблицы ASCII. Таким образом, строки S и Р могут содержать любые символы. Первоначально все байты кодовой таблицы заполняются значением, равным длине строки-образца для поиска Р. Далее последовательно извлекаются символы строки-образца Р начиная с первого. Для каждого символа определяется позиция его самого правого вхождения в строку-образец Р. Это значение и заносится в таблицу D на место, соответствующее этому символу. Подробнее получить представление о заполнении таблицы можно по фрагменту программы на псевдоязыке:
//этап 1: формирование массива d .ДЛЯ j-О ДО 255 ДЕЛАТЬ НАЧ_БЛ0К_1 d[j]:-M К0Н_БЛ0К_1
ДЛЯ j=0 ДО М-2 ДЕЛАТЬ НАЧ_БЛОК_1
d[p[j]]:-M-j-l КОН_БЛОК_1
Так, для строки abcdabce процесс и результаты формирования таблицы D показаны на рис. 4.2.
Куда в двух последних программах пристроить цепочечные команды? К сожалению, некуда. Честно говоря, когда автор писал текст этих программ, он настолько увлекся, что напрочь забыл как о них, так и о цели настоящего раздела — показать особенности использования этих команд при организации поиска информации. А когда вспомнил, то сделал вывод, что пристроить их вроде бы и некуда. А вы как думаете? Окончательный вывод об эффективности можно сделать по результатам работы профайлера.
Развитие этой темы лежит в плоскости обсуждения проблемы обработки файлов, к которой мы когда-нибудь вернемся. 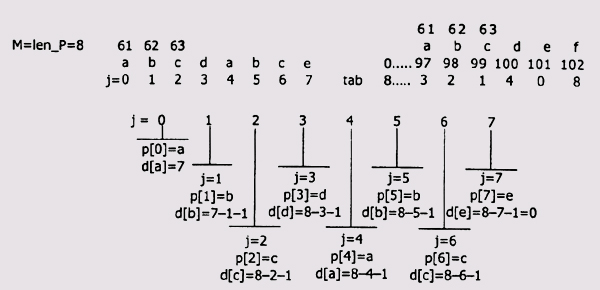
Рис. 4.2. Формирование массива D в программе БМ-поиска |





